ESTADISTICA BÁSICA
Mag. Alvaro Acosta Agón
|
Video: TABLAS DE FRECUENCIAS – Datos agrupados y
No agrupados |
Video: MEDIDAS DE TENDENCIA CENTRAL: Media,
Mediana y Moda |
|
Video: MEDIDAS DE POSICIÓN: Cuartiles, Deciles y
Centiles |
Video: CALCULAR CUARTILES |
|
Video: MEDIDAS DE DISPERSIÓN: Desviación media,
varianza, desviación estándar y coeficiente de variabilidad |
|
1.1 DEFINICIÓN
“Una onza de técnica de
estadística exige una onza de sentido común para su correcta aplicación”
Los orígenes de la estadística están asociados al conteo de personas, riquezas y productos de una colectividad.
En la actualidad, la
estadística se ha convertido en un método efectivo para describir con exactitud
los valores de datos económicos, sociales, psicológicos, biológicos y físicos,
y sirve como herramienta para relacionar y analizar dichos datos.
La ESTADÍSTICA es la ciencia de los DATOS: recolecta, organiza e
interpreta.
Definir la
estadística es una tarea difícil pues habría que precisar en cada una de las
técnicas que se emplean en los diferentes campos en los que interviene. Sin
embargo, en forma general, se dan algunas definiciones.
La Estadística
es una rama de las matemáticas que se encarga de los métodos y procedimientos
para recopilar, organizar, resumir, hallar regularidades, analizar y procesar
datos con el propósito de inferir las características de la población objeto de
estudio, con la finalidad de tomar decisiones y formular predicciones, con base
en los resultados.
La estadística
es una herramienta imprescindible de todas las ciencias, y no se trata de
discutir si es una ciencia, una técnica o una herramienta, sino de la
utilización de sus métodos en provecho del desarrollo del conocimiento.
1.2 DIVISIÓN DE LA ESTADÍSTICA
En resumen, la
Estadística Descriptiva es cuando los resultados del análisis no pretenden ir
más allá del conjunto de datos (tablas, gráficos, cálculos de promedios, varianzas), y la Estadística Inferencial cuando el objetivo
del estudio es generalizar a toda una población desde los resultados obtenidos
de una muestra de datos.
El DANE informa
que Colombia ocupa el puesto 28 del ranking de 196 estados con un número de
habitantes significativos. La población en los últimos cinco años es:
48.203.000 en 2015, 48.748.000 en 2016, 49.292.000 en 2017, 49.834.000 en 2018
y 50.374.000 en 2019. (ESTADÍSTICA DESCRIPTIVA).
Una encuesta mostró que sólo el 46% de los estudiantes de undécimo grado podían resolver problemas que incluyeran fraccionarios, decimales y porcentajes. Además, sólo el 77% de los estudiantes de undécimo grado pudo sumar correctamente el costo de hamburguesas, papas fritas y gaseosas, que figuraban en el menú de un restaurante. (ESTADÍSTICA INFERENCIAL).
APLICACIONES
Contesta las siguientes preguntas:
1.
¿Dónde en nuestras vidas encontramos las estadísticas?
2.
¿Cómo me pueden afectar?
3.
¿Cómo puedo interactuar con ella?
4.
¿Cómo se utilizan en el área que estudio?
1.3 DEFINICIÓN DE TÉRMINOS
· POBLACIÓN: Es el conjunto formado por un grupo de
individuos o elementos, bien definidos, sobre los cuales se pretende estudiar
alguna característica.
TIPOS DE POBLACIÓN:
POBLACIÓN FINITA: Es aquella que
indica que es posible alcanzarse o sobrepasarse al contar. Posee o incluye
un número limitado de medidas y observaciones.
POBLACIÓN INFINITA: Es infinita si se
incluye un gran conjunto de medidas y observaciones que no pueden alcanzarse en
el conteo. Son poblaciones infinitas porque hipotéticamente no existe límite en
cuanto al número de observaciones que cada uno de ellos puede generar.
· MARCO MUESTRAL o MARCO DE REFERENCIA: Es el mecanismo o material que permite delimitar o identificar en forma
apropiada los elementos de una población.
Ejemplo de lista de
unidades o los elementos del muestreo:
En la primera etapa se
realiza la estratificación de las manzanas a nivel de localidad y grupo socioeconómico.
La segunda etapa
consiste en la selección de las viviendas enlistadas al interior de cada
manzana por medio de un muestreo aleatorio.
· MUESTRA: Es una parte o subconjunto representativo de la
población que se selecciona del marco muestral para obtener información.
En la estadística se recogen datos de una muestra. Se utiliza
esta información para
hacer referencias sobre la población que está representada por la muestra. En
consecuencia, muestra y población son conceptos relativos. Una población es
un todo y una muestra es una fracción o segmento de ese todo.
La muestra puede ser aleatoria, tomada al azar y sin la intervención de las personas encargadas de la investigación. Si una muestra es representativa de una población se pueden sacar conclusiones importantes acerca de esta población. Sin embargo, es importante notar que la muestra debe ser aleatoria, porque de otra manera, la inferencia acerca de la población será inválida.
· MUESTREO
ALEATORIO o PROBABILÍSTICO: En una muestra seleccionada por muestreo
aleatorio todos los elementos de la muestra tienen la misma posibilidad de ser
escogidos.
ALEATORIO SIMPLE: Le da la posibilidad a cada uno de los miembros de una población a ser elegidos, si no se
cumple este requisito, se dice que la muestra es viciada. Es uno de los más empleados
y recomendado en las investigaciones sociales y educacionales, ya que permite
obtener conclusiones en la muestra e inferir lo que pudiera ocurrir, a partir
de ésta, en la población, con un elevado grado de pertinencia.
Ejemplo:
Para poder elegir 10 estudiantes de un salón, aleatoriamente se numeran y se
someten al procedimiento.
En
un recipiente se colocan en pedazos de papel los nombres de los estudiantes y se
revuelven, de ahí, la primera tira seleccionada determina el primer estudiante
elegido, no se regresa al recipiente y después de revolver otra vez se
selecciona el segundo estudiante que determina el segundo elegido; el proceso
continúa hasta obtener los diez que se desean elegir.
ALEATORIO SISTEMÁTICO: Se elige el primer individuo al
azar y el resto viene condicionado por aquél.
Se hace una lista de la población a intervalos fijos, bien sea tomando
el coeficiente de elevación (ce) como punto de partida; donde:
Si la población P = 100 elementos y la muestra n= 20, entonces:
Indica que cada vez que
se produzcan piezas en múltiplos de 5, será seleccionada una para la
realización de determinada medición, etc. elementos u
objetos producidos (si se tratara de un proceso de producción de piezas).
Ejemplo:
Para obtener una muestra de suscriptores telefónicos en una ciudad grande,
puede obtenerse primero una muestra aleatoria de los números de las páginas del
directorio telefónico; luego se elige un valor para la muestra. Se realiza el cociente
entre estos dos datos y de acuerdo a este resultado se toman las páginas que
correspondan a los múltiplos del número obtenido.
Ejemplo: Se quiere una muestra
sistemática del 4%, localizas el primer ítem entre un entero entre 1 y 25
(100/4 = 25). Suponiendo que se escoge aleatoriamente el 20, es decir que el primer
valor estará ubicado en la posición 20 en el marco muestral. El segundo valor
estará en la posición 45 (20+25=45); el tercer valor en la posición 65 (45+20=65),
etc., hasta que la muestre esté completa.
Ejemplo: De 250 ovejas, se deben examinar 61 de estas. Se toma un número entre uno y el cuatro. Entonces, tomamos la oveja número 3, y a continuación cada cuarto animal: 7, 11, 15, 19, 23, así sucesivamente hasta llegar a la 247.
ALEATORIO ESTRATIFICADO: Consiste en la división previa de la población de estudio en grupos o clases que se suponen homogéneos con respecto a alguna característica de las que se van a estudiar. A cada uno de estos estratos se le asignaría una cuota que determinaría el número de miembros del mismo que compondrán la muestra. Dentro de cada estrato se suele usar la técnica de muestreo sistemático, una de las técnicas de selección más usadas en la práctica.
En un estudio
de las características socioeconómicas de una ciudad los estratos pueden ser
los barrios de la misma, ya que los barrios suelen presentar características
diferenciales.
Ejemplo: para un estudio de
opinión, puede resultar interesante estudiar por separado las opiniones de
hombres y mujeres.
Se
quiere obtener una muestra de las opiniones de los docentes de una universidad.
Puede ser difícil obtener una muestra con todos los profesores, así que se elige
una muestra aleatoria de cada escuela, o departamento académico; los estratos serían
las escuelas, o departamentos académicos.
ALEATORIO CONGLOMERADOS: La
población está subdividida por subpoblaciones o conglomerados, que son
parecidos entre sí. La selección es al azar: (Estudiantes del mismo curso,
familias nucleares, etc).
Equivalente a las muestras aleatorias estratificadas. Se fijan cuotas de "individuos", especificando las características: solteros, con hijos, estudiante que portan el cabello largo.
· MUESTREO NO ALEATORIO: Es una
muestra seleccionada por muestreo de juicio que se basa en la experiencia de
alguien con la población.
MUESTREO
POR ACCIDENTE (CONVENIENCIA):
Lo que es conveniente para el investigador, este
método incluye los casos más convenientes en su muestra y excluye de ella los
casos inconvenientes. La muestra se obtienen sin ningún
plan, es elegida producto de circunstancias casuales.
Se trata de un proceso en el que el investigador selecciona directa e
intencionadamente los individuos de la población. El caso más frecuente de este
procedimiento es utilizar como muestra los individuos a los que se tienen fácil
acceso, empleada
por algunas agencias de publicidad y de estudios de mercado.
Los pacientes que asistan a una clínica en
particular cierto día de la semana, pueden ser requeridos para
participar.
MUESTREO
INTENCIONAL o JUICIO: El muestreo intencional
es un procedimiento que permite seleccionar los casos característicos de la
población. La lógica y el sentido común pueden usarse para seleccionar la muestra
que sea representativa de la población.
Es muy frecuente su
utilización en sondeos preelectorales de zonas que en anteriores votaciones han
marcado tendencias de voto.
MUESTREO
POR CUOTAS: Facilitar al
entrevistador el perfil de las personas que tiene que entrevistar dejando su
criterio, la elección de las mismas,
Consiste en un número
de individuos que reúnen unas determinadas condiciones, por ejemplo: 20
individuos de 25 a 40 años, de sexo femenino y residentes en Barrancabermeja,
una vez determinada la cuota, se eligen los primero que se encuentren que
cumplan esas características. Este método se utiliza mucho en las encuestas de
opinión.
·DATOS: Son las observaciones
recolectadas: mediciones, géneros o respuestas de encuesta.
TIPOS DE DATOS:
PARÁMETRO: Es una medición numérica que describe algunas características de una población.
El presidente recibió el 50,12% de 18.865.900
votos.
ESTADÍSTICO: Es una medición
numérica que describe algunas características de una muestra.
En una muestra de 200 personas encuestadas, se
encontró que el 45% de ellos no tienen empleo.
La edad promedio registrada en una encuesta a
150 estudiantes es de 16 años.
|
Tipos de Estadísticos
Centralización
Indican valores con respecto a lo que los datos parecen agruparse.
Media, Mediana y Moda
Posición
Dividen un conjunto ordenado de datos en grupos con la misma
cantidad de individuos.
Cuantiles, percentiles, cuartiles, deciles, …
Dispersión
Indican la mayor o menor concentración de los datos con respecto a
las medidas de centralización.
Desviación típica, coeficiente de variación, rango, varianza.
Forma
Dan una idea de cómo se distribuyen los datos.
Asimetría, apuntamiento o curtosis
|
· VARIABLES ESTADÍSTICAS (o datos): Se refiere a una característica o cualidad de un individuo (personas, animales o cosas) que está propenso a adquirir diferentes valores.
Una variable es una característica que va a ser estudiada
en una población. Una variable es estadística si puede ser escrita como una
pregunta cuyas respuestas pueden ser tabuladas o clasificadas dentro de
determinados rangos.
Las variables estadísticas se construyen de acuerdo con el
objetivo del estudio y apuntan a recolectar la información de manera eficaz y
efectiva.
Otra forma de
clasificación de los datos: Escalas
ESCALA
NOMINAL:
|
Nombres o Categorías
Género (hombre/mujer); Raza; Estado Civil; Religión. |
ESCALA
ORDINAL:
|
Cuando siguen un orden
Clasificación de una prueba (primero, segundo, tercero); Estatus socioeconómico; Calificación del cliente (MS, S, I, MI) |
ESCALA
o NIVEL DE MEDICIÓN DE INTERVALO:
|
No tienen un punto de partida inherente, pero la
diferencia entre dos valores de datos tiene un significado. (Los años 1000, 1492,
1776, 2000); (98,2°F y 98,6°F).
|
ESCALA
o NIVEL DE MEDICIÓN DE RAZÓN:
|
Si tiene un punto de partida o cero inherente. (El precio
de un texto escolar, $100.000; un libro de $100.000 es cinco veces más
costoso que un texto de $20.000).
|
Resolver las siguientes situaciones
Un fabricante de medicamentos está interesado en la
proporción de personas que padecen hipertensión (presión arterial elevada) cuya
condición pueda ser controlada por un nuevo producto desarrollado por la
empresa. Se condujo un estudio en el que participaron 5000 personas que padecen
de hipertensión, y se encontró que 80% de las personas pueden controlar su
hipertensión con el medicamento. Suponiendo que las cinco mil personas son
representativas del grupo con hipertensión, conteste las siguientes preguntas:
- Cuál es la
población c.
Cuál es la muestra
- Identifique
el parámetro de interés d.
Identifique la estadística
............................................................................................
Clasificar la siguiente
lista de variables si son estadísticas o no, y además cuáles son discretas o continuas:
a)
Preferencia por algún
deporte
b)
Opinión sobre la situación
económica del país
c)
Razones por las cuales
apoya a un candidato a la Alcaldía
d)
Personas con quien vive
en casa
e)
La infidelidad en
Barrancabermeja.
............................................................................................
La fábrica de gaseosas La Sed proyecta lanzar al
mercado un nuevo sabor. Se realiza un test de aceptación de dicho sabor a 20
niños, utilizando una escala de 10 puntos, para medir el grado de aceptación.
Uno de los niños (Juanito) aceptó el nuevo sabor con 7 puntos. Los puntos
obtenidos en los 19 niños restantes son los siguientes:
2,6,7,4,5,5,9,8,7,1,8,4,7,7,7,6,5,4.
La muestra estuvo compuesta por igual número de niños de
ambos sexos, de 6 a 12 años, pertenecientes a una escuela de Valledupar, los cuales,
en su mayoría, dieron una aceptación de 7 puntos.
- Cuál es la
población c.
Cuál es la muestra
- Cuál es la
variable d. Qué tipo de variable
............................................................................................
Determinar si el valor
dado es un estadístico o un parámetro:
a)
El Senado actual de
Colombia consta de 76 hombres y 32 mujeres
b) Se selecciona una
muestra de estudiantes y el número promedio de textos comprados en este
semestre es 0,25
c) Es un estudio de los
2223 pasajeros del Titanic, se encontró que 706 sobrevivieron cuando se hundió.
d) Cuando se probaron
19.218 máscaras antigás en el ejército de Estados Unidos, se encontró que
10.322 estaban defectuosas.
............................................................................................
Cuál de los cuatro
niveles de medición (nominal, ordinal, de intervalo o de razón) es el más
apropiado:
a)
Las estaturas de los
hombres que juegan basquetbol en la NBA.
b)
Las temperaturas
actuales en los salones de clase de la Universidad.
c)
Los números de las
camisetas de los hombres que juegan en la Liga Postobón.
d)
Las calificaciones de
bueno, regular, fantástico, pobre es citas a ciegas.
e) El número de respuestas
«SI», cuando se les pregunto a 1.250 conductores si alguna vez han hablado por
celular mientras manejan.
1.4 PENSAMIENTO CRÍTICO
El
pensamiento crítico se refiere a la habilidad consciente, sistemática y
deliberada que usa el hombre en la toma de decisiones.
Aprender sin pensar es
trabajar en vano”. Confucio.
Tomado del
Texto Estadística, de Mario Triola.
El éxito del curso de estadística por lo regular requiere
de más sentido común que destreza
matemática. (“El sentido común no es muy común”. Voltaire).
Ahora con los computadores, las aplicaciones modernas de
las estadísticas ya no requieren que dominemos algoritmos complejos de
operaciones matemáticas. En su lugar, nos enfrentamos a la interpretación de datos y los resultados.
Hace cerca de un siglo, el estadista Benjamin Disraeli
pronunció la famosa frase: “Hay tres clases de mentiras: mentiras, viles
mentiras y estadísticas”. También ha dicho: “las cifras no mienten, los mentirosos
calculan las cifras”.
El historiador Andrew Lang dijo que algunas personas
utilizan la estadística “como un borracho utiliza los postes del alumbrado
público: como apoyo, más que como iluminación”.
El caricaturista Don Wright dice: “retome el misterio de la
vida: mienta a un encuestador”.
El autor Franklin P. Jones, escribió que: “la estadística
puede usarse para sustentar cualquier cosa, en especial a los estadísticos”.
En el Esar Comic Dictionary definen que un estadístico es:
“un especialista que reúne pensamientos y los conduce al extravío”.
Hay métodos estadísticos que se utilizan en forma errónea,
de manera que resultan engañosos en última instancia:
1. El intento malintencionado por parte de personas
deshonestas.
2. Los errores de descuido, cometidos por personas que no
conocen nada mejor.
La invitación es asumir un pensamiento crítico, debemos
tener una habilidad para distinguir entre conclusiones estadísticas que parecen
ser válidas de las que son gravemente defectuosas.
Utilice el pensamiento crítico para desarrollar una
conclusión alternativa.
1. Un estudio demostró que los
conductores de camiones «pesan» más que los adultos que no manejan camiones.
Conclusión: Los camiones causan que la gente gane peso.
2. Un estudió concluyó que los
propietarios de casas tienden a vivir más tiempo que quienes no habitan
viviendas propias. Conclusión: Poseer más de una casa crea paz y armonía internas
que causan que las personas tengan mejor estado de salud y vivan más tiempo.
3. Un estudio mostró que en el ciudad de B….. Se
expidieron más comparendos por infracciones de tránsito, a los hombres que a las mujeres. Conclusión:
En la ciudad de B…. Las personas del sexo masculino infringen en mayor número
que las mujeres, las normas de tránsito.
4. Un estudio concluyó que
en la ciudad de Barrancabermeja se expidieron más multas por exceso de
velocidad a personas que conducían automóviles modelos 2013. Conclusión: En la
ciudad de Barrancabermeja, las personas que conducen automóviles modelos 2013,
exceden los límites de velocidad permitidos, caso contrario ocurren con los
otros modelos.
5. Después del último censo realizado, un periódico
tituló: «42.888.592 en Colombia».
6. En un estudio de síntomas del resfriado, se encontró
que cada uno de los sujetos de estudio con resfriado mejoró en dos semanas
después de tomar miel de abejas. Conclusión: La miel de abejas cura el
resfriado.
7. Un periódico afirma que en
los paraderos de buses se causan atracos, porque un estudio concluyó que las
tasas de robos son más altas en las ciudades con paraderos de bus, que en las
zonas rurales que carecen de ellos.
8. María está
analizando la posibilidad de la apertura de una tienda de detalles y regalos.
Se informa en la Cámara de Comercio sobre cuántos establecimientos de esta
clase existen en la ciudad. La información preliminar dice que hay pocos y
presentan una rentabilidad del 50%. Le sugieren que si se especializa en pocas
líneas la rentabilidad será mayor y por ende tendrá un éxito indiscutible. ¿Cómo
debería proceder María para la toma de una decisión correcta?
9. Realizar cualquier actividad deportiva, por
lo menos dos veces a la semana ayuda a que tengamos una vida más saludable, da
energía, evita la depresión y alarga los años de vida.
1.5 PORCENTAJES
1.6 FRECUENCIAS
Uno de los primeros pasos que
se realizan en cualquier estudio estadístico es la tabulación de resultados, es
decir, recoger la información de la muestra resumida en una tabla en la que a
cada valor de la variable se le asocian determinados números que representan el
número de veces que ha aparecido, su proporción con respecto a otros valores de
la variable, etc. Estos números se denominan frecuencias: Así
tenemos los siguientes tipos de frecuencia:
1.6.1 Frecuencia Absoluta
La frecuencia absoluta de una variable estadística es el
número de veces que aparece en la muestra dicho valor de la variable, se
representará como ni.
1.6.2 Frecuencia Relativa
La frecuencia absoluta, es una medida que está influida
por el tamaño de la muestra, al aumentar el tamaño de la muestra aumentará
también el tamaño de la frecuencia absoluta. Esto hace que no sea una medida
útil para poder comparar. Para esto es necesario introducir el concepto
de frecuencia relativa, que es el cociente entre la frecuencia
absoluta y el tamaño de la muestra. Se denota con por fi.
1.6.3 Porcentaje de Datos
La frecuencia relativa es un tanto por
uno, sin embargo, hoy día es bastante frecuente hablar siempre en
términos de tantos por ciento o porcentajes, por lo que esta medida
resulta de multiplicar la frecuencia relativa por 100. Se denotar con pi (%).
1.6.4 Frecuencia Absoluta Acumalada
La frecuencia absoluta acumulada de un valor de la
variable, es el número de datos que hay en el intervalo más las frecuencias
absolutas de los intervalos anteriores y la representaremos por Ni.
1.6.5 Frecuencia Relativa Acumalada
Al igual que en el caso anterior la frecuencia relativa
acumulada es la frecuencia absoluta acumulada dividido por el tamaño de la
muestra, y se denota Fi.
1.6.6 Porcentaje de Datos Acumulados
Análogamente se define el Porcentaje Acumulado y lo vamos
a denotar por Pi como la frecuencia relativa acumulada
por 100.
TABLA DE FRECUENCIA DE DATOS NO AGRUPADOS
TABLA DE FRECUENCIAS PARA DATOS AGRUPADOS
Para el diseño de
las tablas de frecuencia de datos agrupados, se requiere conocer el número de
intervalos y tamaño de cada intervalo.
NÚMERO
DE INTERVALOS o GRUPO (Intervalos de Clase)
Se saca la raíz cuadrada al número total de datos obtenidos.
El valor se aproxima al menor entero. (Para datos menores a 100).
Para datos mayores
de 100, se sugiere utilizar la fórmula de Sturges:
m = número de intervalos de clase
n = número de elementos de la muestra
TAMAÑO DEL INTERVALO (Anchura del Intervalo)
LIMITE DE UN
INTERVALO
El número menor se
denomina límite inferior (L1) y el número mayor límite superior (L2). L1 – L2.
AMPLITUD DEL
INTERVALO DE CLASE:
Es la diferencia entre dos límites inferiores consecutivos:
Cuando no escribe la notación del intervalo [ ), posiblemente el cálculo de la amplitud no es correcto.
MARCA DE CLASE: xi
DENSIDAD DE FRECUENCIA:
Se llama
densidad de frecuencia absoluta de un intervalo, al cociente entre la frecuencia absoluta del intervalo y su amplitud. Se
denota por di.
Aunque no es obligatorio, siempre será conveniente ordenar
de manera ascendente los datos que se tengan
................................................................................................................
..................................................................................................
Los datos
siguientes corresponden al tiempo necesario para procesar 25 tablas en el
computador.
1,17
|
1,61
|
1,16
|
1,38
|
3,53
|
1,23
|
3,76
|
1,94
|
0,96
|
0,15
|
2,41
|
0,71
|
0,02
|
1,59
|
0,19
|
0,82
|
0,47
|
2,16
|
0,92
|
0,75
|
2,59
|
3,07
|
1,4
|
4,75
|
2,01
|
Número de Intervalos:
Tamaño del Intervalo:
Observación: el tamaño o amplitud se expresa con dos decimales, ya que la tabla inicial de datos los contiene.
................................................................................................................
Concentraciones de calcio de 40 análisis
de agua:
Número de Intervalos:
Tamaño del Intervalo:
Observación: el tamaño o amplitud se expresa como un número entero, ya que
la tabla inicial de datos los contiene.
......................................................................................................................................
Mediciones
de 40 eventos:
..............................................................................................................
La concentración de sólidos suspendidos en agua de un
río es una característica ambiental importante. Un artículo científico reportó
sobre la concentración (en partes por millón, o ppm) para varios ríos
diferentes. Supongamos que se obtuvieron las siguientes 60 observaciones para
un río de la ciudad de Barrancabermeja:
55.8
|
60.9
|
37.0
|
91.3
|
65.8
|
42.3
|
33.8
|
60.6
|
76.0
|
69.0
|
45.9
|
39.1
|
35.5
|
56.0
|
44.6
|
71.7
|
61.2
|
61.5
|
47.2
|
74.5
|
83.2
|
40.0
|
31.7
|
36.7
|
62.3
|
47.3
|
94.6
|
56.3
|
30.0
|
68.2
|
75.3
|
71.4
|
65.2
|
52.6
|
58.2
|
48.0
|
61.8
|
78.8
|
39.8
|
65.0
|
60.7
|
77.1
|
59.0
|
50.5
|
69.3
|
70.8
|
64.9
|
37.1
|
87.1
|
66.3
|
62.8
|
60.5
|
39.9
|
80.1
|
62.6
|
60.2
|
50.3
|
38.9
|
70.0
|
65.6
|
xi
|
ni
|
fi
|
%
|
Ni
|
Fi
|
%
|
|
30 – 39
|
34,5
|
8
|
0,1333
|
13,33
|
8
|
0,1333
|
13,33
|
40 – 49
|
44,5
|
10
|
0,1666
|
16,66
|
18
|
0,3
|
30
|
50 – 59
|
54,5
|
8
|
0,1333
|
13,33
|
26
|
0,4333
|
43,33
|
60 – 69
|
64,5
|
20
|
0,3333
|
33,33
|
46
|
0,7666
|
76,66
|
70 – 79
|
74,5
|
9
|
0,15
|
15
|
55
|
0,9166
|
91,66
|
80 – 89
|
84,5
|
3
|
0,05
|
5
|
58
|
0,9666
|
96,66
|
90 – 99
|
94,5
|
2
|
0,0333
|
3,33
|
60
|
1
|
100
|
60
|
0,9999
|
99,999
|
xi
|
ni
|
fi
|
%
|
Ni
|
Fi
|
%
|
|
30,0 – 39,2
|
34,6
|
9
|
0,15
|
15
|
9
|
0,15
|
15
|
39,3 – 48,5
|
43,9
|
9
|
0,15
|
15
|
18
|
0,3
|
30
|
48,6 – 57,8
|
53,2
|
6
|
0,1
|
10
|
24
|
0,4
|
40
|
57,9 – 67,1
|
62,5
|
19
|
0,316
|
31,6
|
43
|
0,716
|
71,6
|
67,2 – 76,4
|
71,8
|
10
|
0,166
|
16,6
|
53
|
0,882
|
88,2
|
76,5 – 85,7
|
81,1
|
4
|
0,066
|
6,6
|
57
|
0,95
|
95
|
85,8 - 95
|
90,4
|
3
|
0,05
|
5
|
60
|
1
|
100
|
60
|
0,9999
|
99,999
|
DISEÑO ADECUADO DE LA TABLA DE FRECUENCIAS:
................................................................................................................
TALLER DE TABLAS DE FRECUENCIAS
(1). El número de hermanos de los
estudiantes de una clase es el siguiente:
0 1 0 0 3 2 1 4 0 0 1 1 2 0 1
1 2 0 1 1 2 1 3 0 0 2 1 2 3 5
a) Elabora una tabla de frecuencias en las que se incluyan:
frecuencia absoluta, absoluta acumulada, relativa y relativa acumulada.
b) Realiza un análisis de los datos obtenidos, que tenga
relación a:
¿Qué porcentaje de
estudiantes son hijos únicos?
¿Cuántos estudiantes
tienen más de un hermano?
(2). En un estudio estadístico sobre el
número de horas que duran 12 pilas de una determinada marca se obtuvieron los
siguientes datos:
10, 12, 12, 11, 12, 10,
13, 11, 13, 11, 13, 9
a) Agrupar los datos en una tabla de frecuencias y
porcentajes.
(3). Los sueldos, en miles de dólares
mensuales de 40 ingenieros de producción en la industria petrolera del año
2019 son:
a).
Elabora una tabla de frecuencias
b). Se
quiere analizar si realmente son bastante altos estos salarios
(6). Estos son los puntajes obtenidos
por los 100 aspirantes que se presentaron para el concurso de las becas
internacionales:
a).
Elabora una tabla de frecuencias
b). Se
quiere analizar qué porcentaje logró clasificar, si el puntaje mínimo requerido
es de 60 puntos.
....................................................................................................................................
TALLER DE TABLAS DE FRECUENCIAS
(1). Dado el siguiente cuadro estadístico con ancho de clase
constante igual a 20. Completar la tabla
[L2 – L1)
|
ni
|
Ni
|
fi
|
%
|
10
|
||||
18
|
||||
35
|
||||
13
|
||||
200)
|
||||
4
|
70
|
(2). Completar los datos que faltan en la siguiente tabla de
frecuencia
xi
|
ni
|
Ni
|
fi
|
1
|
4
|
0,08
|
|
2
|
4
|
||
3
|
16
|
0,16
|
|
4
|
7
|
0,14
|
|
5
|
5
|
28
|
|
6
|
38
|
||
7
|
7
|
45
|
|
(3). Completar la siguiente tabla de frecuencia
para datos agrupados
Intervalos
|
Marca
de Clase
|
Frecuencia
Absoluta
|
Frecuencia
Acumulada
|
Frecuencia
Relativa
|
Frecuencia
Relativa Acumulada
|
[80 –
90)
|
85
|
0,150
|
|||
[90 –
100)
|
8
|
||||
[100
– 110)
|
105
|
23
|
0,225
|
0,575
|
|
[110
– 120)
|
0,825
|
||||
[120
– 130)
|
125
|
7
|
|||
Total
|
40
|
1.0
|
(4).
Los datos que se dan a continuación corresponden a los pesos en Kg. de 80
personas:
60; 66; 77; 70; 66; 68; 57; 70; 66; 52; 75;
65; 69; 71; 58; 66; 67; 74; 61; 63; 69; 80; 59; 66; 70; 67; 78; 75; 64; 71; 81;
62; 64; 69; 68; 72; 83; 56; 65; 74; 67; 54; 65; 65; 69; 61; 67; 73; 57; 62; 67;
68; 63; 67; 71; 68; 76; 61; 62; 63; 76; 61; 67; 67; 64; 72; 64; 73; 79; 58; 67;
71; 68; 59; 69; 70; 66; 62; 63; 66;
a). Elabora una tabla de frecuencias
b). Calcular los porcentajes de personas con pesos
menores a 65 kg y mayores de 80 kg.
1.7 GRÁFICOS ESTADÍSTICOS
1.7.1 Diagramas de Barras
Un diagrama de barras se utiliza para presentar datos
cualitativos o datos cuantitativos de tipo discreto.
Se representan sobre unos ejes de coordenadas, en
el eje de abscisas se colocan los nombres de la variable, y
sobre el eje de ordenadas las frecuencias absolutas, relativas o
acumuladas.
Los datos se representan
mediante barras de una altura proporcional a
la frecuencia.
Consiste en dos ejes perpendiculares y una barra o
rectángulo para cada valor de la variable. Normalmente, se suele colocar en el
eje horizontal los valores de la variable (aunque también se puede hacer en el
vertical). El otro eje se gradúa según los valores de las frecuencias. La
representación gráfica consiste en dibujar una barra o un rectángulo para cada
uno de los valores de la variable de altura igual a su frecuencia.
(1). Todas las barras deben ser del mismo ancho
para no confundir al lector.
(2). Los espacios entre barras deben ser igual
a la mitad del ancho de las barras.
(3). Se deben incluir las escalas y algunas
indicaciones para que ayuden a la lectura de las gráficas.
(4). Los ejes de las gráficas se deben identificar
en forma clara.
(5). Se deben incluir dentro del cuerpo de la
gráfica, o debajo, todo tipo de "claves" para la interpretación de
las gráficas.
Ejemplo:
Un estudio
hecho al conjunto de los 20 estudiantes de un salón de clases para determinar
su grupo sanguíneo ha dado el siguiente resultado:
1.7.2 Polígonos de Frecuencia
Un polígono de frecuencias se forma uniendo los extremos de
las barras mediante segmentos.
También se pueden realizar trazando los puntos que
representan las frecuencias y uniéndolos mediante segmentos.
Para construir un polígono de frecuencia cuando se tienen
datos agrupados, se toma la marca de clase, que coincide con el punto medio de
cada rectángulo.
1.7.3 Histogramas
Un histograma es una representación
gráfica de una variable en forma de barras.
Se utilizan para variables continuas o
para variables discretas, con un gran número de datos, y que se han
agrupado en clases.
En el eje abscisas se construyen
unos rectángulos que tienen por base la amplitud del intervalo,
y por altura, la frecuencia absoluta de cada intervalo.
Es un caso particular de variables continuas, si los
intervalos son correlativos, los rectángulos aparecen pegados en la
representación gráfica. En caso de que la amplitud de los intervalos no se
igual para todos, hay que hacer coincidir el área del rectángulo con la
frecuencia del intervalo. Un ejemplo muy utilizado de histograma es una
pirámide de población.
Se
obtiene “el peso” a 65 estudiantes a través de la siguiente tabla:
En las variables
cuantitativas o en las cualitativas ordinales se pueden representar polígonos de frecuencia
en lugar de histogramas, cuando se representa la frecuencia acumulativa, se
denomina ojiva.
DISTRIBUCIONES
SIMÉTRICAS Y ASIMÉTRICAS: Una distribución es simétrica si los lados
derecho e izquierdo del histograma son aproximadamente imágenes especulares el
uno del otro. Una distribución es asimétrica hacia la derecha si el lado
derecho del histograma (que contiene la mitad de las observaciones mayores) se
extiende mucho más lejos que el lado izquierdo. Una distribución es asimétrica
hacia la izquierda si el lado izquierdo del histograma se extiende mucho más
allá que el lado derecho.
1.7.4 Diagramas de Sectores
Un diagrama de sectores se puede utilizar para
todo tipo de variables, pero se usa frecuentemente para las variables
cualitativas.
Los datos se representan en un círculo, de modo que el
ángulo de cada sector es proporcional a la frecuencia absoluta correspondiente.
El diagrama circular se construye con la ayuda de un transportador.
Ejemplo: Un curso está conformado
por 30 estudiantes. De los cuales 14 juegan futbol, 8 practican voleibol, 6
juegan basquetbol y los demás no practican ningún deporte.
1.7.5 Pictogramas
Son gráficos con dibujos alusivos al carácter que se
está estudiando y cuyo tamaño es proporcional a la frecuencia que representan;
dicha frecuencia se suele representar.
En el siguiente ejemplo hemos representado el número
de partidos ganados, perdidos o empatados de un equipo.
1.7.6 Cartogramas
Son gráficos realizados sobre mapas, en los que
aparecen indicados sobre las distintas zonas cantidades o colores de acuerdo
con el carácter que representan.
Las medidas de
tendencia central, llamadas así porque tienden a localizarse en el centro de la
información. Permiten condensar, en un único valor los resultados
obtenidos para la totalidad de la muestra y en relación con cada una de las
variables consideradas. Ese valor pretende reproducir el comportamiento
mayoritario de la muestra.
Al describir grupos de observaciones, con frecuencia es conveniente
resumir la información con un solo número. Este número que, para tal fin, suele
situarse hacia el centro de la distribución de datos se denomina medida o parámetro
de tendencia central o de centralización.
Cuando se hace referencia únicamente a la posición de estos parámetros
dentro de la distribución, independientemente de que ésta esté más o menos
centrada, se habla de estas medidas como medidas de posición.
Entre las medidas de tendencia central se tienen:
2.1 MEDIA ARITMÉTICA
La media aritmética es el valor obtenido en la
suma de todos sus valores dividida entre el número de sumandos. Se le
llama también promedio o, simplemente, media.
Estas son las
cinco (5) notas que un estudiante obtuvo en determinada asignatura: 3.5; 3.1;
2,7; 3,8; 2,1. Calcular la media de estos datos.
2.1.1 Media Aritmética para datos agrupados
En un test realizado a un grupo de 40 personas se han obtenido las
puntuaciones que muestra la tabla. Calcula la puntuación media.
Dos maneras de calcular la media aritmética para datos agrupados: utilizando las frecuencias absolutas:
Cálculo de la media para datos agrupados, utilizando las frecuencias relativas:
2.1.2 Otros tipos de Medias
2.1.2.1 Media Aritmética Ponderada
Suponga que un auto cubre los primeros
100 km a una velocidad de 60 km/h, los siguientes 100 km a 70 km/h y los
últimos 100 km a 80 km/h. Calcular, la velocidad media realizada.
TALLER DEL CÁLCULO DE DIVERSAS MEDIAS
2.2 MEDIANA
2.3.1 Mediana para datos agrupados
2.1.2.1 Media Aritmética Ponderada
La media ponderada permite calcular un promedio
que toma en cuenta la importancia de
cada valor con respecto al total.
Se denomina media ponderada de un conjunto de
números al resultado de multiplicar cada uno de los números por un valor
particular para cada uno de ellos, llamado peso, y obteniendo a continuación,
la media aritmética del conjunto formado por los productos anteriores.
Nota: se utiliza la media ponderada cuando no
todos los elementos componentes de los que se pretende obtener la media tienen
la misma importancia.
Un estudiante
obtuvo 40, 50, 60, 80 y 45 puntos en las asignaturas de Matemáticas,
Estadística, Física, Química y Biología respectivamente, suponiendo que los
pesos de cada una son: 5, 2, 4, 3 y 1.
Las notas de la Universidad donde el
primer corte vale 30% de la nota final, otro el 35% y el último 35%. Las notas
obtenidas por un estudiante en la asignatura de estadística fueron: 2.2, 3.4 y
3.1.
En una empresa hay 5 trabajadores que ganan $2.000.000;
4 ganan que $2.500.000; 8 que ganan $1.750.000 y 3 que ganan $3.000.000. ¿Cuál
es el promedio de salarios de la empresa?
2.1.2.2 Media Aritmética Geométrica
La media geométrica es un promedio muy útil en conjuntos de
números que son interpretados en orden de su producto, no de su suma. Por ejemplo,
las velocidades de crecimiento.
Se tienen la
siguiente serie de números: 15, 20, 25, 30, 35 y 40. Hallar la media aritmética
y la media geométrica.
En una empresa quieren saber la proporción
media de mujeres en las diferentes áreas. Para ello, se conocen los siguientes datos:
Producción: 32,6%; Compras: 53,5%; Marketing: 28,9%, Recursos Humanos: 48,2% y
Administración 67,4%.
2.1.2.3 Media Armónica
Se utiliza cuando se desea promediar velocidades, cuando el
tiempo se mantiene constante y las distancias varían o también son constantes.
Si la velocidad
de A a B es de en 60 km/h y de B a A es 30 km/h, ¿Cuál es su velocidad
promedio?
2.1.2.4 Media Cuadrática
Se usa en
aplicaciones de la física y en la determinación de las características de
dispersión.
TALLER DEL CÁLCULO DE DIVERSAS MEDIAS
(1). En la tabla
se muestran la resistencia de 70 baldosas. Hallar la media de este grupo de
datos agrupados:
Resistencia
(Kg/cm2)
|
ni
|
|
[100 a 200)
|
6
|
|
[200 a 300)
|
8
|
|
[300 a 400)
|
21
|
|
[400 a 500)
|
33
|
(2). La tabla
muestra los años de experiencia de 50
operarios de una fábrica de confecciones.
Calcular la media aritmética.
4
|
6
|
5
|
6
|
4
|
5
|
5
|
6
|
5
|
6
|
5
|
5
|
8
|
8
|
8
|
9
|
6
|
7
|
7
|
6
|
7
|
9
|
3
|
2
|
7
|
5
|
7
|
7
|
3
|
4
|
6
|
7
|
7
|
7
|
8
|
6
|
6
|
7
|
6
|
3
|
4
|
6
|
8
|
5
|
6
|
7
|
5
|
5
|
4
|
6
|
(3). Las calificaciones de un estudiante están conformadas
por los siguientes factores: Un examen cuyo valor es 40% en el cual obtuvo una
nota de 4.5; un trabajo de consulta con ponderación del 10% y calificación de
1.0; una exposición equivalente al 15% con nota de 2.0; y por último una
investigación con valor del 35% calificada con 3.5. Calcular la nota definitiva
del primer corte.
(4). Durante 4 meses consecutivos una persona compra
combustible para su automóvil a los precios de $8.500, $8.700, $8,950 y $9.000
por un galón. Se compra 20 galones cada mes.
¿Cuál
fue el promedio del costo del combustible para el período de 4 meses?
¿Calcular
la media geométrica para el costo del combustible?
¿Hallar
la media armónica para el costo del combustible?
2.2 MEDIANA
La mediana es un valor
de la variable que está en la mitad de los datos, una vez que éstos están
ordenados de menor a mayor.
En caso de un número
par de datos, la mediana no correspondería a ningún valor de la variable, por
lo que se conviene en tomar como mediana el valor intermedio entre los dos
valores centrales.
- Si el número de valores es impar, la Mediana corresponderá al valor central de dicho conjunto de datos.
- Si el número de valores es par, la Mediana corresponderá al promedio de los dos valores centrales (los valores centrales se suman y se dividen por 2).
Para calcular únicamente
la posición (medidas de posición) de estos parámetros dentro de la
distribución:
2.2.1 Mediana para datos agrupados
La mediana se encuentra en el intervalo donde la frecuencia acumulada
llega hasta la mitad de la suma de las frecuencias absolutas. Es decir, se
tiene que buscar el intervalo en el que se encuentre:
Li
es el límite inferior de la clase
donde se encuentra la clase mediana.
N/2 es
la semisuma de las frecuencias absolutas.
Ni-1
es la frecuencia acumulada anterior
a la clase mediana.
ai es
la amplitud de la clase.
Calcular la mediana de
una distribución estadística que viene dada por la siguiente tabla:
.........................................................................................
..............................................................................................
2.3 MODA
Unimodal: 5,7,4,6,9,5,6,1,5,3,7. El número
que más se repite es 5, entonces la moda es 5.
Bimodal de los datos,
cuando se encuentran dos modas, es decir, dos datos que tengan la misma
frecuencia absoluta máxima.
Multimodal: cuando en
una distribución de datos se encuentran tres o más modas.
Por último, si todas
las variables tienen la misma frecuencia, entonces no hay moda.
Para
el cálculo de la Moda, no es necesario ordenar
los datos.
103, 101, 99, 101, 87,
95, 99, 101
Mo = 101
2.3.1 Mediana para datos agrupados
Li Límite
inferior de la clase modal
D1 Frecuencia de
la clase modal menos la frecuencia de la clase anterior
D2 Frecuencia de
la clase modal menos la frecuencia de la clase siguiente
ai Amplitud
de la clase modal
La siguiente tabla representa el tiempo en segundos en que se utilizan
los cajeros de un centro comercial de la ciudad durante el mes anterior.
TALLER DE MEDIDAS DE TENDENCIA CENTRAL
Observaciones de las MEDIDAS DE TENDENCIA CENTRAL
MEDIA ARITMÉTICA:
Su resultado es sensible ante la presencia de valores
extremos (bajos o altos). Su aplicación es aconsejable cuando los datos son bastante
homogéneos.
MEDIANA:
Presenta el
inconveniente de que en su cálculo no intervienen todas las observaciones sino
únicamente las observaciones centrales. Es aconsejable su utilización cuando
los datos son irregulares.
MODA:
Su aplicación es
apropiada cuando algún valor absorbe la mayor parte de las frecuencias, esto
es, la mayoría de las observaciones son iguales entre sí. Un inconveniente es
que existan varios valores modales.
MEDIA GEOMÉTRICA:
Es apropiada cuando la
variable tiene un carácter acumulativo. Carece de sentido si hay algún valor
nulo o si se presentan simultáneamente valores positivos y negativos.
MEDIA ARMÓNICA:
Su interpretación no es
tan clara. Aunque utiliza todos los datos, presenta inconveniente de que es muy
sensible ante la presencia de valores bajos.
.............................................................................................................
VIDEO: MEDIDAS DE TENDENCIA CENTRAL: MEDIA, MEDIANA Y MODA
Autor: Alvaro Acosta Agón
YouTube: https://youtu.be/05nA1KVXRXs
............................................................................................................
Las medidas de posición dividen un conjunto de datos en grupos con el mismo número de individuos.
Para calcular las medidas
de posición es necesario que los datos estén
ordenados de menor a mayor.
Las medidas de
posición son:
3.1 CUARTILES
Los cuartiles son
los tres valores de la
variable que dividen a
un conjunto de datos ordenados en cuatro partes iguales.
Q1, Q2 y
Q3 determinan
los valores correspondientes al 25%
(¼), al 50% (½) y al 75% (¾) de los datos.
1. Ordenamos los datos de menor a mayor
2. Buscamos el lugar que ocupa cada cuartil
El número de orden del
primer cuartil (Q1)
es igual al número de términos de la distribución más uno, sobre cuatro.
Para el segundo cuartil
(Q2) el número de orden se
calculará sumando uno al total de términos y dividiéndolo entre dos.
Asimismo, el número de
orden del tercer cuartil (Q3) ser igual a tres cuartos del número de términos de la distribución más
uno.
3, 4, 5, 7, 8, 10, 11
3, 4, 5, 7, 9, 10, 11, 14
2, 3, 5, 6, 7, 8, 12, 20
Nota: Una
vez obtenido el número de orden del primer cuartil, se puede calcular
inmediatamente los del segundo y tercer cuartil sin recurrir al procedimiento
arriba sugerido, multiplicándolo por dos y tres respectivamente.
Se registran las siguientes variaciones de
temperaturas a presión atmosférica: 41°, 50°, 29°, 33°, 40°, 42°, 53°, 35°,
28°, 39°, 37°, 43°, 34°, 31°, 44°, 57°, 32°, 45°, 46°, 48°.
28°, 29°, 31°,
32°, 33°, 34°,
35°, 37°, 39°, 40°, 41°, 42°, 43°, 44°, 45°, 46°, 48°, 50°, 53°, 57°
N°Q1 = (N+1)/4 = (20+1)/4 = 5,25 Q1
= 33°
N°Q1 = k (N/4) = 1(20/4) = 1(5) = 5 Q1 = 33°
La posición 5, corresponde al dato Q1 = 33
N°Q2 = (N+1)/2 = (20+1)/2 = 10,5 Q2
= 40°
N°Q2 = k (N/4) = 2(20/4)
= 2(5) = 10 Q2
= 40°
La posición 10, corresponde al dato Q2 = 40
N°Q3 = 3(N+1)/4 = 3(20+1)/4 = 15,75 Q3 = 45°
N°Q3 = k (N/4) = 3(20/4)
= 3(5) = 15 Q3
= 45°
La posición 15, corresponde al dato Q3 = 45
Nota: Como los cuartiles representan un posición: 25%, 50% y 75%, cuando el número de esta posición del cuartil da un resultado decimal, entonces se aproxima a la posición entera.
3.1.1 Cuartiles para datos agrupados
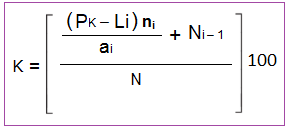
Li límite inferior de la clase donde se encuentra el cuartil
N
la suma de las frecuencias
absolutas
Ni-1 la frecuencia acumulada anterior
a la clase del cuartil
ai la amplitud de la clase
ni frecuencia absoluta
En primer lugar, se busca la clase donde se encuentra, en la tabla de las frecuencias acumuladas (Ni).
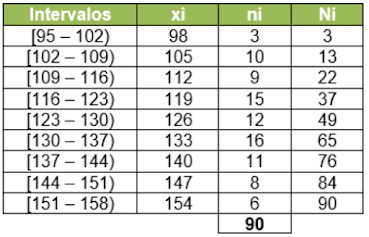
La tabla muestra los puntajes en las Pruebas Saber, de
60 estudiantes:
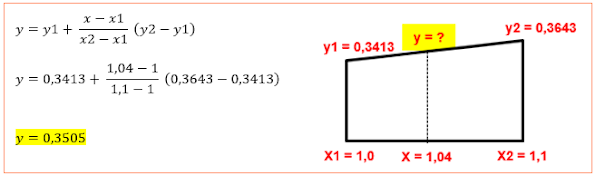
INTERPOLACIÓN LINEAL
Es para calcular un valor intermedio de una recta cualquiera, definida
por dos puntos conocidos. Denominada como una “regla de cinco”, donde se definen
cinco valores: dos de cada punto conocido, además de la abscisa u ordenada del
punto deseado.
TALLER DE CUARTILES
(1).
Encontrar los cuartiles (Q1, Q2 y Q3) de una muestra de 15 mediciones de
sólidos suspendidos, en unidades de mg/L, de una muestra de agua residual.
1, 4, 4, 5, 7, 8, 10, 12, 17, 19,
19, 21, 27, 29, 30
(2). Halar los cuartiles Q1, Q2 y Q3, de acuerdo a los
siguientes datos:
10, 13, 4, 7, 8, 11, 10,
16, 18, 12, 3, 6, 9, 9, 4, 13, 20, 7, 5, 10, 17, 10, 16, 14, 8, 18
3). Calcular los cuartiles Q1, Q2 y Q3 para datos agrupados, de acuerdo a las siguientes tablas:
Intervalos
|
xi
|
ni
|
Ni
|
[10, 15)
|
12,5
|
4
|
4
|
[15, 20)
|
17,5
|
3
|
7
|
[20, 25)
|
22,5
|
7
|
14
|
[25, 30)
|
27,5
|
8
|
22
|
[30, 35)
|
32,5
|
4
|
26
|
26
|
Intervalos
|
ni
|
Ni
|
[50, 60)
|
8
|
|
[60, 70)
|
10
|
|
[70, 80)
|
16
|
|
[80, 90)
|
14
|
|
[90, 100)
|
9
|
|
[100, 110)
|
2
|
|
[110, 120)
|
1
|
|
(4).
Los datos siguientes corresponden a los tiempos de reacción de una muestra de
33 sujetos, medidos en centésimas de segundo:
55,
51, 60, 56, 64, 56, 63, 63, 61, 57, 62, 50, 49, 70, 72, 54, 48, 53, 58, 66, 68,
45, 74, 65, 58, 61, 62, 59, 64, 57, 63, 52, 67.
Calcule
el primer, segundo y el tercer cuartil, a partir de una tabla de datos
agrupados.
........................................................................................................................................................
3.2 DECILES
Los deciles o decillas dividen la información en diez partes iguales, en cantidades porcentuales de 10 en 10.
D1
|
D2
|
D3
|
D4
|
D5
|
D6
|
D7
|
D8
|
D9
|
D10
|
10%
|
10%
|
10%
|
10%
|
10%
|
10%
|
10%
|
10%
|
10%
|
10%
|
El quinto decil
corresponde a la mediana.
Para calcular la posición en la que se encuentra cada
uno de los deciles Dx,
se utiliza la siguiente fórmula:
Como en la posición 2,4
no coincide con un dato y está dentro de dos valores iguales a 25, entonces no
hay necesidad de interpolar, por lo tanto:
D1 = 25
Decil 2:
Decil 7:
3.2.1 Deciles para datos agrupados
El quinto decil
corresponde a la mediana.
Se tienen los
siguientes resultados:
28
|
31
|
28
|
30
|
28
|
27
|
30
|
32
|
35
|
26
|
25
|
29
|
26
|
28
|
25
|
31
|
31
|
32
|
27
|
30
|
31
|
31
|
25
|
28
|
Calcular los deciles
D1, D2 y D7
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
25
|
25
|
26
|
26
|
27
|
28
|
28
|
28
|
28
|
28
|
29
|
30
|
30
|
30
|
30
|
31
|
31
|
31
|
31
|
31
|
32
|
32
|
35
|
Decil 1:
Como en la posición 4,8
no coincide con un dato y está dentro de dos valores iguales a 26, entonces no
hay necesidad de interpolar, por lo tanto:
D2 = 26
Como en la posición
16,8 no coincide con un dato y está dentro de dos valores: 30 y 31, entonces
hay necesidad de interpolar, usando proporcionalidad. Pero teniendo en cuenta
que es una posición tomamos que en la posición 17, está el dato 31.
16
|
16,8
|
17
|
30
|
?
|
31
|
Hallar el D7 para la siguiente tabla de frecuencias
La fórmula más
utilizada para calcular la posición del percentil es: P (n + 1).
Los percentiles
(centiles) dividen la información en cien partes iguales, lo cual facilita la
interpretación porcentual de una distribución de frecuencias.
El percentil 50 corresponde
a la mediana.
P es el percentil cuya posición
se quiere calcular dividido entre 100
n es el número de casos
3, 4,
7, 8, 9
Calcular P25 (C1)
P (n + 1) 0,25 (6) = 1,5
1,5 es la posición, que indica
que el punto medio entre el primer y segundo dato.
P25 = 3,5
Calcular P50 (C2) (Mediana)
P (n + 1) 0,5 (6) = 3
3 es la posición del dato.
P50 = 7
Calcular P75 (C3)
P (n + 1) 0,75 (6) = 4,5
4,5 es la posición, que indica
que el punto medio entre el cuarto y quinto dato.
P75 = 8,5
3.3.1 Percentiles para datos agrupados
El intervalo en el que se encuentra el percentil K se
denomina intervalo crítico.
Una
distribución estadística viene dada por la siguiente tabla:
Hallar los percentiles 15 y 70
Calcular el percentil
10 de acuerdo a la tabla siguiente:
Intervalos
|
xi
|
ni
|
Ni
|
[1 –
4)
|
2
|
2
|
2
|
[4 – 7)
|
5
|
5
|
7
|
[7 – 10)
|
8
|
6
|
13
|
[10 –
13)
|
11
|
7
|
20
|
[13 –
16)
|
14
|
9
|
29
|
[16 –
19)
|
17
|
10
|
39
|
[19 –
22)
|
20
|
11
|
50
|
50
|
Cuando se calcula el percentil que corresponde a una puntuación determinada, el resultado puede dar decimal, entonces se toma la cantidad entera más próxima, ya que los percentiles son 99 valores enteros.
Nota: En
los diversos ejercicios resueltos en los apartados anteriores se han utilizado
fórmulas para datos ordenados y tabulados, siguiendo reglas para el número de
intervalos y tamaño del mismo. Pero, cuanto se tienen datos numerosos no hay unanimidad
para su cálculo entre los diferentes autores, por eso el valor de un determinado
percentil de un conjunto de datos puede ser diferente al utilizar distintos
programas informáticos.
RELACIÓN ENTRE LAS MEDIDAS DE POSICIÓN
TALLER DE DECILES Y PERCENTILES
Calcular los deciles 2 y 8 de la distribución de la
tabla:
Intervalos
|
ni
|
Ni
|
[50, 60)
|
8
|
|
[60, 70)
|
10
|
|
[70, 80)
|
16
|
|
[80, 90)
|
14
|
|
[90, 100)
|
9
|
|
[100, 110)
|
2
|
|
[110, 120)
|
1
|
|
Calcular los deciles 3 y 6 de la distribución de la
tabla:
Intervalos
|
xi
|
ni
|
Ni
|
[10, 15)
|
12,5
|
3
|
|
[15, 20)
|
17,5
|
5
|
|
[20, 25)
|
22,5
|
7
|
|
[25, 30)
|
27,5
|
4
|
|
[30, 35)
|
32,5
|
2
|
|
21
|
En la siguiente tabla, que
no fue diseñada de acuerdo a la Ley de Sturges, se presentan las respuestas a
una prueba de 80 preguntas aplicadas a 500 personas. Hallar los percentiles:
Intervalos
|
ni
|
[0, 10)
|
21
|
[10, 20)
|
28
|
[20, 30)
|
81
|
[30, 40)
|
87
|
[40, 50)
|
112
|
[50, 60)
|
78
|
[60, 70)
|
54
|
[70, 80)
|
39
|
Total
|
500
|
Calcular los percentiles 30 y 90
Qué percentil le correspondería al que tenga 65 respuestas
correctas.
.............................................................................................................
VIDEO: MEDIDAS DE POSICIÓN: CUARTILES, DECILES y PERCENTILES
Autor: Alvaro Acosta Agón
YouTube: https://youtu.be/JVGmZHwE1rs
............................................................................................................
En el análisis estadístico
no basta el cálculo e interpretación de tendencia central o de posición, ya
que, cuando se representa toda una información con la media aritmética, puede
estar distante a la realidad, pues suelen existir datos extremos inferiores y
superiores a la media aritmética, los cuales, no están siendo bien
representados por este parámetro.
Las medidas de dispersión resumen la heterogeneidad de
los valores de la variable. En algunos casos, indican qué tan alejados están
los valores respecto de un punto de referencia o de un eje.
Para medir el grado de dispersión de una variable, se
utilizan principalmente los siguientes indicadores:
4.1 RANGO o RECORRIDO
Es la diferencia de la variable entre sus valores máximo y mínimo de los datos de una distribución estadística.
4.4.1 Rango o Recorrido Intercuartílico (RQ)
Es la diferencia entre los cuartiles mayor y menor.
Con esta medida se excluyen los valores más altos y
bajos, pues elimina el 25% de los valores más altos y el 25% de los valores más
bajos de la distribución.
4.4.2 Rango o Recorrido Intercuartílico Medio [(RQ)/2]
Es el valor medio de la diferencia entre el mayor y
menor cuartil.
4.2 DESVIACIÓN MEDIA
La desviación media,
mide la distancia absoluta promedio entre cada uno de los datos, y el parámetro
que caracteriza la información. Usualmente se considera la media aritmética
de los valores absolutos de las desviaciones respecto a la media.
Calcular la desviación media de los siguientes datos:
2, 4, 6, 8
Calcular la desviación
media de la distribución:
9,
3, 8, 8, 9, 8, 9, 18
Calcular la desviación media de la distribución de datos agrupados:
Calcular la desviación media de la distribución de datos agrupados:
Calcular la desviación media de la distribución de datos agrupados:
4.3 VARIANZA
Calcular la varianza muestral de
la distribución:
9,
3, 8, 8, 9, 8, 9, 18
El problema de los signos en la desviación media, es eludido elevando las diferencias al cuadrado. La varianza es uno de los parámetros más importantes, pues teniendo conocimiento de la varianza de una población, se ha avanzado en el conocimiento de la población misma.
La variancia sesgada o varianza poblacional, refleja a la perfección el significado de una medida de dispersión como un promedio de los cuadrados de las desviaciones y tiene una gran aplicación en el estudio de las probabilidades.
Se define la varianza,
como desviación cuadrática media de los datos con respecto a la media
aritmética.
Las fórmulas de la varianza poblacional y la varianza de la muestra son
ligeramente diferentes
La variancia
insesgada, varianza muestral o cuasivarianza, es más propicia en los cálculos
estadísticos y se usa en las muestras.
Cuando
el tamaño de la muestra es grande, (n – 1) será aproximadamente igual a n, por
lo que este denominador tiene un impacto real en el cálculo de la varianza para
muestras pequeñas.
Calcular la varianza de acuerdo con la tabla de datos agrupados
Otras fórmulas equivalentes para
calcular la varianza en datos agrupados:
xi
|
ni
|
xi · ni
|
xi2 · ni
|
|
[10,
20)
|
15
|
1
|
15
|
225
|
[20,
30)
|
25
|
8
|
200
|
5000
|
[30,40)
|
35
|
10
|
350
|
12 250
|
[40,
50)
|
45
|
9
|
405
|
18 225
|
[50,
60
|
55
|
8
|
440
|
24 200
|
[60,70)
|
65
|
7
|
455
|
29 575
|
[70,
80)
|
75
|
6
|
450
|
33 750
|
49
|
2315
|
123 225
|
Propiedades de la Varianza (s2)
La varianza será
siempre un valor positivo, o cero en el caso que las puntuaciones sean iguales.
La varianza, al igual
que la media, es un índice muy sensible a las puntuaciones extremas.
La varianza no viene
expresada en las mismas unidades que los datos, ya que las desviaciones están
elevadas al cuadrado.
4.4 DESVIACIÓN TÍPICA
Para una mejor comprensión se debe recurrir a la
desviación típica o estándar, definida como la raíz cuadrada de la varianza.
4.5 COEFICIENTE DE VARIABILIDAD
En una muestra aleatoria normal se
tomaron los siguientes resultados: 41.9, 45.2, 45.8, 45.8, 45.9, 46.0, 46.1,
46.1, 46.4, 47.0. Calcular la desviación típica.
Generalmente interesa
establecer comparaciones de la dispersión, entre diferentes muestras que posean
distintas magnitudes o unidades de medida.
El coeficiente de
variabilidad tiene en cuenta el valor de la media aritmética, para establecer
un número relativo, que hace comparable el grado de dispersión entre dos o más
variables.
El coeficiente de
variación permite comparar las dispersiones de dos distribuciones distintas,
siempre que sus medidas sean positivas.
Se calcula para cada
una de las distribuciones y los valores que se obtienen se comparan entre sí.
Una distribución tiene x = 140 y s = 28,28 y otra x = 150 y s = 25. ¿Cuál de las dos distribuciones presenta mayor dispersión?.
:::::::::::::::::
En una
distribución discreta se tiene los siguientes valores: –10, 3, x, 10, 1,
0. Si la desviación típica es igual al coeficiente de variación, calcular el
valor desconocido de x.
:::::::::::::::::
::::::::::::::::
Calcular el coeficiente de variabilidad en la siguiente distribución:
xi | ni | xi | (xi)2 |
2 | 2 | 4 | 8 |
3 | 5 | 15 | 45 |
4 | 7 | 28 | 112 |
5 | 2 | 10 | 50 |
Total | 16 | 57 | 215 |
.............................................................................................................
VIDEO: MEDIDAS DE DISPERSIÓN
Autor: Alvaro Acosta Agón
YouTube: https://youtu.be/G592FbUsMeY
............................................................................................................
EJERCICIOS RESUELTOS DE LAS
MEDIDAS DE DISPERSIÓN
5.1 PRINCIPIO FUNDAMENTAL DEL CONTEO
Supongamos que se está en la ciudad A y para trasladarse
a la ciudad B tiene dos caminos. Una vez que está en B puede viajar a C
por tres vías diferentes. ¿De cuántas maneras diferentes puede viajar de A a C?
Se puede trasladar desde A a C de (2)(3) = 6 maneras
diferentes, es decir, n1 n2 = 6
En
lo que respecta a técnicas de conteo, se tienen dos principios fundamentales:
·
El Principio de Adición
·
El Principio de Multiplicación
5.1 Principio de Adición (o)
Un evento o suceso “A”
ocurre de n maneras y otro “B” ocurre de m maneras. Es decir, ocurre de una
forma u otra, más no de ambas formas a la vez (no suceden en simultáneo).
Número de maneras en
que puede ocurrir el evento A o el evento B es: n + m
María puede ir desde su casa a la universidad tomando un solo
transporte. Si por su casa pasan tres líneas de busetas que la llevan a la
universidad, ¿de cuántas maneras diferentes, según la buseta que tome, llegará
María a la universidad?. Se sabe que la línea A tiene tres busetas, la línea B
tiene 5 busetas y la línea C tiene 8 busetas.
5.1 Principio de Multiplicación (y)
Un evento o suceso “A”
ocurre de n maneras diferentes seguido de otro evento “B” que ocurre de m
maneras distintas. Es decir, ocurre uno a continuación de otro, originando un
suceso compuesto.
Número de maneras en
que puede ocurrir el evento A o el evento B es: n x m
Los estudiantes de una institución educativa se comprometen a pintarlo.
El primer piso lo harían estudiantes de un aula del noveno, el segundo piso lo
haría estudiantes de un aula de décimo, el tercer piso lo harían estudiantes de
un aula de undécimo. Si la institución tiene 4 aulas para noveno, 5 para décimo
y 6 para undécimo. ¿De cuántas maneras distintas, según las aulas que
intervienen, puede hacerse el pintado del colegio?.
EJEMPLO 1: ¿Cuántos números de dos dígitos se
pueden obtener con los siguientes números: 1,3,5,6,8
a). Si se puede repetir cualquier de los dos dígitos
31, 33, 35, 36, 38
51, 53, 55, 56, 58
61, 63, 65, 66, 68
81, 83, 85, 86, 88
Este método es tedioso y extenso, entonces como son dos
números de dos dígitos, se pueden considerar dos eventos n1 n2, así:
n1 = 5 y n2 = 5, porque
ambos eventos se pueden realizar de 5 maneras diferentes. Luego n1 x
n2 = (5) (5) = 25 números que se pueden formar.
b). Si no se permite repetir ninguno de los dos dígitos
31, 35, 36, 38
51, 53, 56, 58
61, 63, 65, 68
81, 83, 85, 86
Para la primera casilla se dispone de todos los cinco
dígitos (n1 = 5). Para la
segunda casilla sólo quedan cuatro alternativas o cuatro números ya que no
permite repetir uno de los dígitos, por esto n2 = 4. De modo
que (5) x (4) = 20 números que se
pueden formar.
EJEMPLO 2: ¿Cuántos números de dos dígitos se
pueden formar que sean pares, si se pueden repetir con los siguientes números:
1,3,5,6,8
16, 18
36, 38
56, 58
66, 68
86, 88
Los únicos pares, de los cinco dígitos anteriores, son el 6
y el 8, por lo que n2 = 2.
n1 = 5, porque se dispone de todos los
cinco dígitos (se permiten números repetidos)
Así que: n1 x
¿Cuántos números de dos dígitos se pueden formar
que sean pares, si no se pueden repetir?
16, 18
36, 38
56, 58
68,
86,
Los únicos pares, de los cinco dígitos anteriores, son el 6
y el 8, por lo que n2 = 2.
n1 = 4, porque al no aceptarse
repeticiones, el número que se utilice en la casilla de la derecha no podrá
repetirse
Así que: n1 x
EJEMPLO 3: El Instituto Nacional de Transporte
y Tránsito le pide que resuelva la siguiente situación: Se desean imprimir
licencias (permisos) de conducción clasificada en seis categorías:
01 motocicletas con motor de 100cc
02 motocicletas con motor de más de 100cc
03 automóviles, camperos, camionetas y
microbuses de servicio particular
04 automóviles, camperos, camionetas y
microbuses de servicio público
05 camiones rígidos, busetas y buses
06 vehículos articulados
Se desea también, que cada categoría conste de
siete dígitos. ¿Cuántas licencias informaría que se deben imprimir por cada
categoría? ¿Cuánto sería el número total?
Con el principio fundamental del conteo se puede resolver
la situación. Para simplificar el problema, se puede calcular, primero el
número de licencias que se deben imprimir para cada categoría y, después,
multiplicar por seis para obtener el número total de licencias.
Número de licencias para cada categoría: Supongamos la
categoría 01, consta de 7 dígitos.
El número 10 que aparece dentro de cada casilla significa
que tiene 10 maneras diferentes para realizar cada evento (del 0 al 9). Como
son 7 eventos, el número de licencias a imprimir, para cada categoría, será: 107
Total de licencias: 6 x 107 = 60 millones
EJEMPLO 4: De cuántas maneras diferentes se
pueden acomodar tres personas en una fila de tres sillas?
Suponga que las personas A, B y C y las sillas 1, 2 y
3. Hay 6 maneras diferentes.
Para la primera casilla tiene tres personas, es decir tres
alternativas. Como en la primera casilla ya acomodó a una persona, de las tres,
en la segunda casilla sólo tiene dos alternativas. En la tercera casilla sólo
tendrá una persona o una opción.
EJEMPLO 5: ¿Cuántas representaciones diferentes serán posibles formar,
si se desea que consten de Presidente, Vicepresidente, Secretario, Tesorero, y Vocal?,
sí esta representación puede ser formada de entre 25 miembros del sindicato de
una pequeña empresa.
25 x 24 x 23 x 22 x 21 = 6.375.600 maneras de formar una representación de ese sindicato que conste de presidente, vicepresidente, secretario, etc.
EJEMPLO 6: ¿Cuántos números de cinco cifras no tienen
cincos ni treses?
Se llenan cinco
espacios _ _ _ _ _. En el primer espacio, de los diez dígitos, no se usa el 3
ni el 5, pero tampoco usar un cero, pues el número tendría menos de cinco
cifras. Entonces se tienen 7 opciones para el primer espacio. En las restantes
4 posiciones se puede colocar cualquier digito excepto el 3 y el 5, es decir 8
opciones en cada caso. El principio de la multiplicación da un total de 7 × 84
= 28.672 números.
EJEMPLO 7: Si hay que escoger un número de cuatro
cifras que tenga todas sus cifras pares excepto cuatros y ochos, o todas sus
cifras impares, excepto cincos y sietes, ¿De cuantas formas puede hacerse?
Hay dos tipos de
números que queremos contar: los que tienen dígitos pares y los que tienen
dígitos impares. El principio de la adición dice que el total lo obtenemos
sumando el total de cada caso.
Cuando todos son
pares, hay cuatro posiciones _ _ _ _. En la primera posición se tiene un número
par que no sea 4 ni 8, pero tampoco cero (porque de lo contrario, el número ya
no tendría cuatro cifras). Entonces se tienen dos opciones (2, 6). Para las
demás posiciones tenemos 3 opciones siempre (2, 6, 0). El total es 2 × 33
= 54.
Cuando todos son
impares, como no se puede poner cincos ni sietes, entonces se tienen 3 opciones
para cada espacio: 1, 3, 9. En total hay 34 = 81 números de esta forma.
Entonces, el
total pedido (usando el principio de la suma) es 54 + 81 = 135.
EJEMPLO 8: ¿Cuántos números de seis cifras hay que no
tienen sus dígitos repetidos?
Tenemos seis
espacios a llenar _ _ _ _ _ _. En el primero, se tienen 9 opciones, porque no se
pueden poner el cero. En la segunda posición también se tienen 9 opciones,
porque, aunque ya no se puede usar el número escogido antes, ahora si se puede usar
el cero. Para la tercera posición se tienen 8 opciones (de los 10 dígitos, ya
usados dos), para la cuarta posición hay 7 opciones, para la quinta 6 y para la
última 5. En total hay 9×9×8×7×6×5= 136.080
números de seis cifras sin dígitos repetidos.
EJEMPLO 9: De Bucaramanga
a Bogotá hay 5 aerolíneas diferentes, ¿de cuántas maneras se puede viajar de
Bucaramanga a Bogotá y regresar en una aerolínea diferente?
5 x 4 = 20
EJEMPLO 10: How many positive 6 digits integers are
there?
9 x 10 x 10 x 10 x 10 x 10 = 900
Nota: Aunque los principios básicos de conteo pueden usarse en la gran mayoría de los casos, usualmente hay fórmulas (basadas en esos principios) que permiten hacer los cálculos de manera más rápida. Otro método práctico es el diagrama de árbol.
En una
heladería se sirven los helados en dos presentaciones: cono o vaso. Y los
sabores que se pueden escoger son: chocolate, vainilla y fresa.
5.2 FACTORIAL
Este
símbolo representa el producto de los números enteros positivos desde n hasta
1, disminuyendo la unidad al entero precedente.
n! = n (n – 1)
(n – 2) …
5!
= 5.4.3.2.1 = 120
EJEMPLO 11: Cinco estudiantes han sido elegidos
en su curso para formar el gobierno escolar y deciden sortear entre ellos los
cargos de: presidente, vicepresidente, secretario, tesorero y vocal. Pueden
efectuar el sortear mediante papeles colocados en una caja con los nombres de
los cargos, para que cada un saque un papel.
¿De cuántas maneras puede quedar constituido el gobierno
escolar?
Cargo Posibilidad
Presidente 5
aspirantes
Vicepresidente 4 aspirantes
Secretario 3 aspirantes
Tesorero 2 aspirantes
Vocal 1 aspirante
5! = 5 x
EJEMPLO 12: Hay cuatro regalos diferentes para entregarlos a cuatro estudiantes que clasificaron a la final de un evento de poesía. El sorteo puede efectuarse por muestreo aleatorio simple.
¿De cuántas maneras pueden entregarse estos
regalos?
4! = 4 x 3 x 2 x 1 = 24
::::::::::::::
EJEMPLO 13: Se tienen los números
naturales: 1, 2, 3 y 4. ¿Cuántos números de cuatro cifras se pueden conformar?
4! = 4 x 3 x 2 x 1 = 24
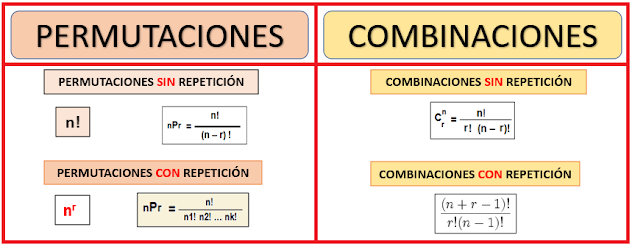
En muchas ocasiones se desea
conocer el número de grupos diferentes que se forman con los datos, sin
especificar cada uno de los elementos.
Si
interesa el orden en la elección de los elementos
No
interesa el orden en que son elegidos los elementos
Si se
devuelven o no los elementos elegidos
“Si me interesa el orden”, significa que si variamos la
posición de los elementos obtendremos grupos diferentes o, también, si
cambiamos el orden de selección, los grupos ya no serán iguales. Se pueden
formar dos palabras con las letras “a” y “b”, ya que la palabra ab
es diferente a la palabra ba.
“No
interesa el orden”,
significa que, si dos grupos tienen los mismos elementos, en diferente
posición, debemos contarlos como uno solo, es decir, que los dos grupos los
consideramos iguales. Cuántas palabras de dos letras puedo formar con las
letras “a” y “b”. Solo se puede formar una palabra, ya que ab =
ba.
Son
las más fáciles de calcular. Si tienes n
cosas para elegir y eliges r
de ellas, las permutaciones posibles son:
n
× n × ... (r veces) = nr
(Se
puede repetir, el orden importa)
Ejemplo 1: en la cerradura hay 10 números para elegir (0, 1,..., 9) y
eliges tres de ellos:
10
× 10 × ... (3 veces) = 103 =
1000 permutaciones
Ejemplo 2: Cuántos números de dos cifras se pueden formar con los 10
dígitos del 0 al 9?
nr = 102
= 100
Como
n = 10 y x = 2, podemos formar 102
= 100 números de dos cifras
El número de permutaciones con
repetición de n
elementos, donde el primer elemento se repite n1 veces; el segundo, n2…; el
último, nk veces, se representa:
Ejemplo
3: Con las letras de la palabra TELÉFONO, ¿Cuántas ordenaciones diferentes se
pueden formar?
Ejemplo
4: María ha invitado a cinco amigas a su casa. Les ofrece algo para beber, pero
en su nevera solo le quedan dos jugos de naranja, tres gaseosas y un yogur. ¿De
cuántas formas pueden repartirse las bebidas entre María y sus cinco amigas?
Ejemplo 5:
Las placas para los autos en un país, consta de tres letras iniciales más
cuatro dígitos: la tercera letra debe ser exclusivamente la b. Calcular el
total de placas que pueden asignarse en esta ciudad.
1 letra 2 letra 3 letra 4
dígito 5 dígito 6 dígito 7 dígito
(26) (26) (1) (10) (10) (10) (10)
(26)*(26)*(1)*(10)4 = 6.760.000
Dados n elementos distintos, el
número de secuencias ordenadas de éstos es:
Pn = n (n – 1) (n – 2) …
Este número también se denota como n!
Ejemplo 6: Cuántas palabras diferentes se pueden formar con las letras n, i, l, o.
(4) * (3) * (2) *(1) = 4! = 24
Ejemplo
7: ¿Ordenar 16 bolas de billar?
Así que tu primera elección tiene
16 posibilidades, y tu siguiente elección tiene 15 posibilidades, después 14,
13, etc. Y el total de permutaciones sería:
16
× 15 × 14 × 13 ... = 20,922,789,888,000
16!
= 20,922,789,888,000
n es el número de cosas que puedes
elegir,
r
las que eliges de ellas
(Nota: no se puede repetir, el orden importa)
Ejemplo 8: Elegir 3 bolas de billar de entre 16.
16
× 15 × 14 = 3360 (principio multiplicativo)
Ejemplo 9: Elegir 3 bolas de billar de entre 16.
n
= 16 r = 3
Ejemplo
10: Si no se permiten números repetidos, en la formación de cada uno de ellos,
¿Cuántos números de 3 dígitos se pueden formar con los siguientes números: 3,
7, 1, 4, 8 y 2?
n = 6 r
= 3
Ejemplo
11: Si no se permiten números repetidos, en la formación de cada uno de ellos, ¿Cuántos
números de tres dígitos se pueden formar con los siguientes números: 0, 1, 2,
3, 4, 5, 6, 7, 8 y 9?
n = 10 r = 3
Ejemplo 12: Si cinco corredores
compiten en la carrera final de los 100 metros, ¿de cuántos modos pueden
ganarse tres premios?
n = 5 r = 3
Ejemplo 13: ¿Cuántas
representaciones diferentes serán posibles formar, si se desea que consten de
Presidente, Secretario, Tesorero, Primer Vocal y Segundo Vocal?, sí esta
representación puede ser formada de entre 25 miembros del sindicato de una
pequeña empresa.
25
x 24 x 23 x 22 x 21 = 6,375,600
(principio multiplicativo)
Ejemplo
14: ¿Cuántas maneras hay de asignar los cuatro primeros lugares de un concurso
de creatividad que se verifica en las instalaciones de nuestra institución, si
hay 14 participantes?
14x13x12x11
= 24,024 (principio multiplicativo)
PERMUTACIÓN CIRCULAR
Para
acomodar n personas en un espacio circular de “n” puestos, se utiliza (n
– 1)!
Ejemplo 15: ¿De
cuántas maneras se pueden ubicar cuatro personas en una mesa circular de 4
asientos?
Pc (4) = (4 – 1)! = 6 maneras
diferente
Ejemplo 16:
¿De cuántas maneras se pueden ubicar nueve personas?
a). En una fila de
nueve puestos:
9! = 362.880
b) En una mesa
circular de 9 asientos:
(n – 1)! =
(8!) = 40.320
c) En una mesa
circular de 9 asientos, donde una persona puede sentarse en cualquier silla:
(1) * (8!) =
40.320
Ejemplo 17: Una empresa está buscando a tres personas para ocupar tres puestos de
igual categoría. Se postulan seis candidatos. ¿Cuántos grupos diferentes de
tres personas se pueden formar con los candidatos?
Ejemplo 19: En un restaurante sirvieron una porción de papas con tres salsas diferentes a elegir entre diez posibles. ¿De cuántas formas diferentes se puede hacer la elección de las salsas?
Ejemplo 20: Elegir 3 bolas de billar de entre 16. (Sin orden)
Ejemplo 21: Elegir 3 bolas de billar de entre 16, da las mismas combinaciones que
elegir 13 bolas de 16.
Ejemplo
22: Se
desea formar algunos comités de profesores para la representación de docentes
ante el consejo directivo. Para la elección de los comités se tienen 7
candidatos: cuatro de matemáticas y tres de física. Un comité consta de tres
personas. ¿Cuántos comités se pueden
formar?
Ejemplo
23: Para decidir los ganadores de un concurso de matemáticas, un profesor
debe elegir de jurado a tres de sus 22 estudiantes. ¿De cuántas formas
diferentes puede realizar su elección?
Ejemplo
24: Se tienen cinco sabores de helados: chocolate, vainilla, fresa, limón y
banana. Puedes tomar tres de ellos. ¿Cuántas combinaciones puedes hacer?
Ejemplo
25: Un pintor que dispone en su paleta de cinco colores: azul, rojo, verde,
blanco y negro; empieza a realizar mezclas de tres colores, iguales o
distintos. ¿Cuántas combinaciones diferentes puede realizar de esta manera?
ESPACIO MUESTRAL (U): Es el conjunto de todos los posibles resultados que se pueden obtener al realizar el experimento. Es todo lo que puede ocurrir al realizar un experimento.
EVENTO (E) o Punto Muestral:
Es un subconjunto del espacio muestral.
La probabilidad de que ocurra un evento se mide por un número entre cero y uno, inclusive. Si un evento nunca ocurre, su probabilidad asociada es cero, mientras que si ocurriese siempre su probabilidad sería igual a uno.
La
probabilidad es la relación entre el número de resultados de éxito respecto al
total de resultados posibles, puede ser objetiva o subjetiva.
Enfoque clásico:
En una caja hay 50 manzanas rojas y 200 manzanas
verdes, cuál es la probabilidad que al tomar una fruta ésta sea manzana roja.
Enfoque de frecuencia
relativa:
En una caja que contiene manzanas rojas y verdes, se
han tomado 80 frutas y de éstas 15 han sido manzanas rojas, cuál es la
probabilidad que al tomar una fruta ésta sea manzana roja.
p:
(probabilidad
de éxito) es la probabilidad que ocurra un evento
q: (probabilidad
de fracaso) es la probabilidad de que no ocurra un evento: q = 1 – p
EVENTOS:
MUTUAMENTE EXCLUYENTES o DISJUNTOS: Aquellos que no pueden ocurrir simultáneamente (al mismo tiempo). Ej: que un billete sea de $5.000 y de $10.000.
NO EXCLUYENTES ENTRE SÍ o COMPATIBLES: Cuando la ocurrencia de uno de ellos no impide que suceda también otro. Ej: que una persona sea profesor y tenga 20 años.
INDEPENDIENTES: Éstos no se ven afectados por otros. El resultado de uno no afecta al otro. Ej: el tipo de ropa y la probabilidad que llueva durante el día.
DEPENDIENTES
Cuando
un evento afecta la probabilidad de que suceda otro. Ej: si un proceso no se
realiza con materiales de calidad, es más probable que el resultado resulte
mal.
Ejemplo
1: Lanzamiento de monedas:
a) Si el experimento se basa en el lanzamiento
de una moneda, el espacio muestral tiene dos elementos, cara (c) y sello (s):
U
= {c, s}
b)
Si se desea que caiga cara en un lanzamiento, entonces el evento tiene una sola
posibilidad:
E
= {c}
Ejemplo 2: Lanzamiento de un dado:
a)
Se lanza un dado, qué probabilidad
existe que el resultado sea impar:
U
= {1,
2, 3, 4, 5, 6}
E
= {1, 3, 5}
Ejemplo 3: Si se
extrae una carta de un paquete de 52 cartas de las cuales 26 son negras (13
espadas A, 2, 3, … , 10, J, Q, K; 13 son tréboles); y 26
son rojas (13 corazones y 13 diamantes), halle la probabilidad de que la carta sea:
a)
Una K
b)
Roja
c) Diamante
Ejemplo
4: Considere el siguiente conjunto de 9 flores: 6 rojas y 3 blancas:
a)
Si se escoge una flor al azar, ¿Cuál es la probabilidad de que sea roja?
b) Si se escoge una flor aleatoriamente, ¿Cuál es la probabilidad de que sea blanca?
Considere el
siguiente conjunto de 9 flores: 6 rojas y 3 blancas:
c)
Si se escoge dos flores aleatoriamente, ¿Cuál es la probabilidad de que ambas
sean rojas?
¿Cuántos
grupos diferentes de dos flores rojas podemos formar con seis flores rojas?
¿Cuántos
grupos diferentes de dos flores podemos formar con un total de 9 flores?
Considere el
siguiente conjunto de 9 flores: 6 rojas y 3 blancas:
d)
Si se escoge cuatro flores, al azar,
¿Cuál es la probabilidad de que dos sean blancas y dos sean rojas?
Para
formar el numerador:
x1
= se escogen dos flores rojas
x2
= se escogen dos flores blancas
Para
el denominador:
¿Cuántos
grupos diferentes de cuatro flores podemos formar con nueve flores?
Ejemplo
5: Hallar la probabilidad de sacar una
suma de 8 puntos al lanzar dos dados.
El
espacio
muestral es:
Ejemplo
6: Hallar la probabilidad de sacar por suma o bien 4, o bien 11 al
lanzar dos dados.
El
espacio
muestral es:
Ejemplo
7: Si se seleccionan dos fichas de una
bolsa que contiene fichas numeradas del 1 al 10, calcular las probabilidades
que:
El
espacio muestral es:
U
= (1,2), (1,3), (1,4), ……. #U = 45 posibilidades
a)
A =
La suma de las dos fichas sea menor que 10
A
= (1,2), (1,3), (1,4), (1,5), (1,6),
(1,7), (1,8), (2,3),
(2,4), (2,5), (2,6), (2,7), (3,4),
(3,5), (3,6), (4,5). #E = 16
Ejemplo 8: ¿Cuál es la probabilidad de sacar dos
bolas negras de una urna que contiene 15 bolas blancas y 12 negras, sin
reintegrar la bola extraída?
Las
12 bolas negras pueden tomar de 2
en 2 de maneras distintas (casos favorables).
Mientras
que las 27 bolas totales pueden
tomarse de 2 en 2 de maneras distintas (casos posibles).
Ejemplo 9: Una bolsa contiene 6 globos rojos, 4
blancos y 5 azules. Se saca al azar un globo. Hallar las siguientes probabilidades,
al ser extraído un globo:
Ejemplo
10: Cuál es probabilidad de obtener un AS
o un REY sacando una sola carta en una baraja española de 40 cartas. Si uno de
los casos aparece, queda excluido el otro.
Ejemplo 11:
En un cofre se tienen seis monedas de: $1000; tres monedas de $500; y una de
$200. ¿Cuál es
la probabilidad que al extraer una moneda, ésta sea de $1000?.
Ejemplo 12:
En un cofre se tienen seis monedas de: $1000; tres monedas de $500; y una de
$200. ¿Cuál es
la probabilidad que al extraer una moneda, ésta sea de $1000 o de $500?.
Ejemplo 13:
Se lanza un dado,
y se gana si el resultado es par o divisible por 3. ¿Cuál es la probabilidad de
ganar?
U = {1, 2, 3,
4, 5, 6}
A = Resultado par: {2, 4, 6}
B = Divisible por tres: {3, 6}
Ejemplo 14:
Cuál es probabilidad
de que carta extraída sea un AS o COPAS
Ejemplo 15:
Se lanza un par de
dados. Si la suma es 6, hallar la probabilidad que uno de los dados sea 2?.
E = Suma sea 6:
{(1, 5), (2, 4), (3,3), (4,2), (5,1)}
A = {dado = 2}
AWE =
{(2, 4), (4, 2)}
Ejemplo
16: Al
lanzar dos dados, ¿Cuál es la probabilidad de sacar dos cincos?
Ejemplo 17:
En un cofre se tienen seis monedas de: $1000; tres monedas de $500; y una de
$200. ¿Cuál es
la probabilidad que al extraer al azar dos monedas, ambas sean de $1000?.
Ejemplo 18: Si se extrae dos cartas de un paquete de 52 cartas, halle la probabilidad de que ambas cartas sean ases, si la primera carta extraída:
Ejemplo 19:
¿Cuál es probabilidad
que un estudiante de la secundaria que juega fútbol compita luego en la liga
nacional y llegue a graduarse como profesional?
P(A) = juega
fútbol, el 5% de los estudiantes de secundaria
P(B) = juega en
la liga profesional, el 1,7%
P(C) = graduado
como profesional, el 40%
P(A) = 0,05
P (B l A) = 0,017
P(C l A y B) =
0,4
P (A y B y C)
= P (A) * P (B l A) =
P(C l A y B)
P (A y B y C) =
(0,05) * (0,017) * (0,4) = 0,00034 = 0,034%
Ejemplo 20:
Si los eventos A y
B son independientes, y P(A) = 0,2 y P(B) = 0,3 hallar lo siguiente:
.....................................................................................................................................
EVALUACIÓN FINAL DE PROBABILIDADES
Ejemplo. De cuántas formar se pueden ordenar en un estante siete libros de: 4 de matemáticas, 2 de Español y 1 de Inglés.
Ejemplo. Con las letras de la palabra CASAS, ¿Cuántas palabras de cinco letras distintas se pueden formar?
Ejemplo. Con las letras de la palabra SALUD, ¿Cuántas palabras de cinco letras distintas se pueden formar?
Ejemplo. Cinco estudiantes se presentaron a un concurso de pintura. El concurso otorga $200.000 al primer lugar, y $150.000 al segundo y $100.000 al tercero. ¿De cuántas formas se pueden repartir los premios de primero, segundo y tercer lugar?
Ejemplo. Se va a programar un torneo de microfútbol para 10 equipos. ¿Cuántos partidos se deben programar si cada equipo jugará con todos, sin partidos de revancha?
Ejemplo. ¿Cuántos grupos de dos elementos se pueden formar de un conjunto que contiene cinco elementos?
Ejemplo. Se han
convocado a 25 jugadores para un equipo de fútbol. ¿Cuántos maneras diferentes
se puede integrar un equipo de 11 jugadores?
Ejemplo. Se disponen de cuatro banderas de colores rojo, amarillo, negro y blanco. ¿Cuántas combinaciones pueden hacerse si es posible colocar en el asta tres banderas?
Ejemplo: Considere el siguiente conjunto de 10 pelotas: 6 pelotas rojas y 4 pelotas azules:
a) Si se escoge una pelota al azar, ¿cuál es la probabilidad de que sea roja?
b) Si se escoge una pelota aleatoriamente, ¿Cuál es la probabilidad de que sea azul?
c) Si se escoge dos pelotas aleatoriamente, ¿Cuál es la probabilidad de que ambas sean rojas?
Ejemplo:
Al
lanzar dos dados, ¿Cuál es la probabilidad de sacar dos cincos?
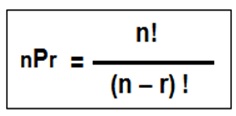
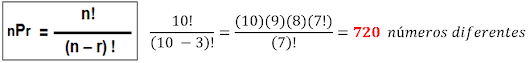
0 Comentarios